DETERMINATION OF LEAST OBSERVATION TIME CLASSIFIED BY BASELINE GRADE ACCORDING TO GPS SATELLITE COMBINATIONProf. Jongchool LEE and Hosik JANG, KoreaKey words: Positioning Error, Least Square Method, Relative Positioning, GPS Satellite Combination, Least Observation Time. AbstractIn the 20th century, there was a remarkable progress in survey instrument and technology powered by the development of scientific technologies. Precision positioning is now possible thanks to GPS (Global Positioning System), three dimensional positioning method using satellites. GPS receiver installed in the observation point and at least four satellites determine the three dimensional coordinates, therefore, disposition and number of the satellites and the baseline may affect the accuracy, and observational error often occurs. This research is to see how earth surface position error changes according to the number and combination of observation satellites through relative location observation method. Least square method is used for position error analysis. It is to analyze what is the minimum observation time when limiting the position error. 1. INTRODUCTIONThe most recent, rapid growth of telecommunication - skill, and a space technique bring remarkable development on a surveying instrument, and sector of surveying technique. It accelerates diversification, and a high level of survey such as GPS survey, the technique using the high resolution of satellite image, GPS technique. Especially, an application of GPS surveying instrument is enlarged more and more in the field of survey from new operation method, using instrument, information propulsion, a safety secure, correspondence to internationalization, and protection of nature environment point of view. GPS stands for Global Positioning System. It sets up three dimension, which you want to observe, the latitude, the longitude , an altitude H, by positioning instrument. The units are degree, minute, second, and meter, and it is divided into point positioning which uses 1 receiver, and relative positioning which uses 2 receiver according to purpose of survey. Method of base line measurement is that of static measurement applied to detailed control point observation. static observation has a problem with taking a lot of time in practical affair because observed time is not steady according to the distance. Accordingly, this research observes how earth surface position changes according to number, and combination of observation satellites through relative positioning, and analysis of positioning error uses the method of least squares. In this analysis effect, in case of setting limits to positioning error, It is to see how much of least observed time may be applied. 2. RELATIVE POSITIONING OF GPSTo use GPS phase observation formula, survey calculation is carried out with the data that records the number of returned wave phase received by GPS receiver. The time of starting survey, the number of wave of carrier that is existed between a satellite and GPS receiver. Namely, phase number is called interger number. If you know this, it is possible to calculate a base-line vector at two point intervals by relative positioning. The problem is that it is hard to count the number of wave because carrier is regular in a type of wave. Therefore, GPS survey calculation is fundamental to what kind of way, and the how little data it needs. The method of relative positioning to calculate interger number are Single Difference, Double Difference, Triple Difference. 2.1 Single differenceAn error term of a satellite clock is eliminated by calculating phase survey formula of 1 satellite / 2 receiver or an error term of receiver clock is eliminated by calculating phase survey formula of 2 satellite / 1 receiver. An orbit error and tropospheric delay error can be reduced if the distance between two receiver is shorter than height of GPS satellite. 2.2 Double differenceRemoving both receiver, and an error term of satellite clock by calculating more than two of single difference, and unknown term will just remain interger number, therefore survey calculation is carried out by an observation equation for 4 of satellites and 3 of double difference. 2.3 Triple differenceTriple difference that subtracts according to continuous time is lower than double difference on an accuracy because of poorness of substance of information. It is used to revise cycle slip which is generated in the middle of surveying. Cycle Slip comes from the case of passing through an obstacle like tree, an active action of ionosphere, or electronic wave obstacle in the area where lots of radio wave emits. 3. COMPUTATION OF OBSERVED VALUE BY THE METHOD OF LEAST SQUARES3.1 Distance error-linear expression up to GPS satelliteIn GPS positioning, To seek location of surveying
position, position of coordinate In general, satellite’s clock and receiver’s clock are
accompanied with a little error. 4 of unknown If distance from surveying point
Supposing, point
Error Equation shows as Eqs(3).
where,
This coefficient of development form term 2~4 from Eqs(2) turns as follow.
Eqs(4) turns Eqs(8) by means of
On survey, supposing distance from surveying point
where
Eqs(10) may be gotten from Eqs(9), and (8)
Revision of satellite clock is monitored by a
tracking station, and transmissive coefficient in the navigational
message from the satellite can be revised by clock corrective
equation. On account of this, value of the left side in Eqs(10) may be
calculated. While, 4 of unknown and, it can be expressed as follow.
3.2 Approximation of positioning value by the method of least squaresBecause linear expression is possible
The method of least squares seeks
After theorem of Eqs(13)~Eqs(16), regular equation may be Eqs(17)~Eqs(20).
Then, a part of coefficient of
From the forth dimensional simultaneous equation, 4. THE METHOD OF SURVEYINGThis research is that the control point being used at Pukyoung National University in Pusan was used, and observed point within the compass of distance 1km, 2.5km, 5km, 7.5km, 10km, 15km, 20km, was selected. as shown Figure 1. The time of survey were 30, 60, 90, and 120 minutes and acquisition space of the data was 30 sec. The distances of rapid static positioning were selected 1km, 2.5km, 5km, 7.5km, 10km, 15km as Method of static positioning, and the time of survey were 5, 10, 15, and 20 minutes and acquisition space of the data was 5 sec. To combine GPS satellite, considering in case of
being getting over 4each of satellites, Since it is possible to see
selection of For example,
Fig.1 A Map of GPS observation points Table 1. The number of combinations of satellite with the number of satellite.
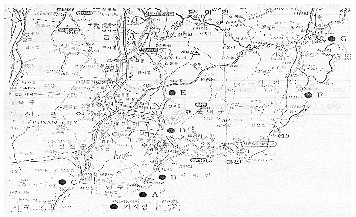
Observed period of GPS is 0.5 Sidereal Day (about 11hours and 58 minutes), so It is 4 minutes faster in a day. We apply static positioning or rapid static positioning belong to relative positioning to observe the same time everyday, and altitude of receiver is 15 degree. Accuracy is estimated as comparison of dimension of absolute observed error, and relative accuracy of distance X, and Y by relative positioning with 2 GPS receivers. Received data is calculated by the method of least squares according to computer process. 5. ANALYSIS OF OBSERVED VALUE5.1 Result of distance observation according to the number of satellite in static positioningAllowable scope error limits absolute observed error to 5mm, and relative accuracy is shown Table 2. Table 2. Control point relative observation allowable error
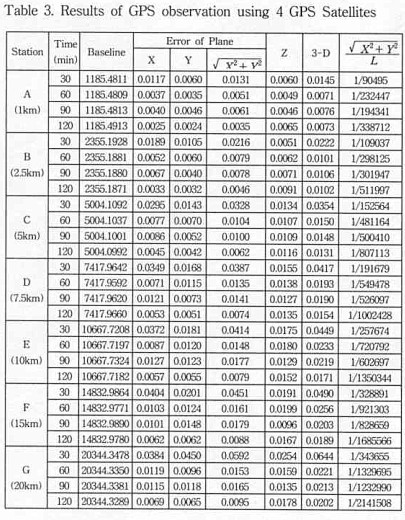
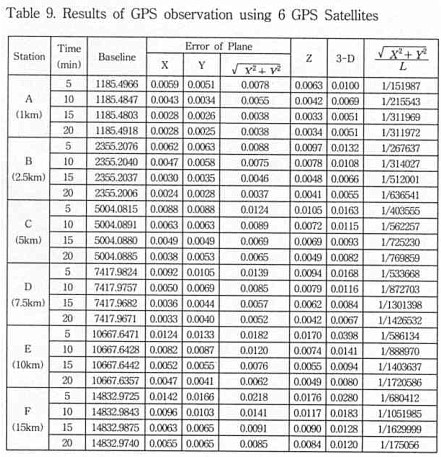
If absolute observed error is limited to 5mm following satellite combinations in distance in static positioning, at the time of that satellite is 4 each, satisfied observation more than 120minutes within shorter than 2.5km, and when the number of satellite are 5, 6 is sufficient over 30 min within 1km, over 60min within 2.5km, and over 120min within 5km. In the case of more than 7, the time of observation needs over 30min within 1km, 60min within 2.5km, and 120min within 10km.
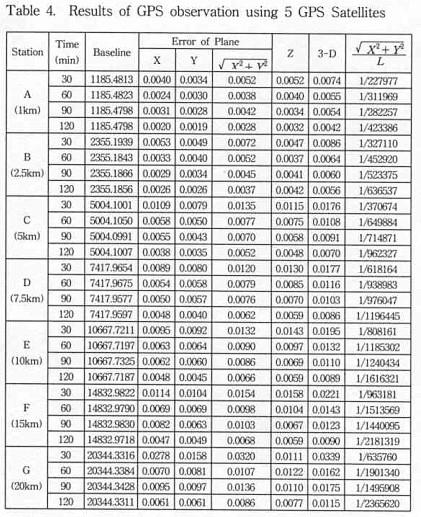
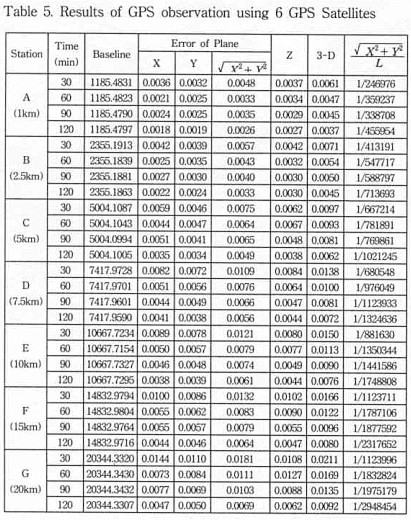
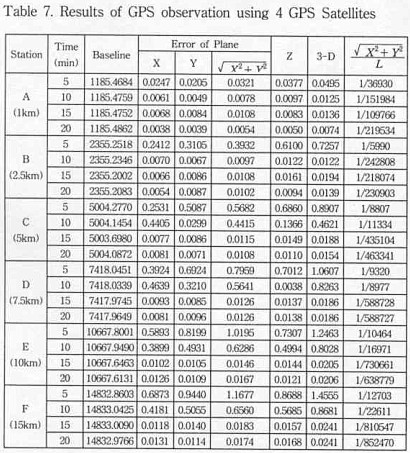
5.2 Result of distance observation according to the number of satellite in rapid static positioningAbsolution observed error is limited to 5mm according to satellite combinations in distance in rapid static positioning, In case of 4 of satellite, the time of observation needs over 20min within 1km. in case of 5 of satellite, the time of observation needs over 10min within 1km, over 20min within 2.5km, and in the case of 6 of satellite, the time of observation needs over 15min within 1km,2.5km, over 20min within 7.5km.
6. CONCLUSIONThis research calculates dimension of observed error followed satellite combination in distance to determine least observed time of baseline classified followed GPS satellite combinations, and To get optimum observed time suited to fiducial point survey, the conclusions was taken as below by static positioning, and rapid static positioning.
CONTACTProf. Jongchool Lee Hosik Jang 19 April 2001 This page is maintained by the FIG Office. Last revised on 15-03-16. |
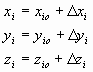 (3)
(3)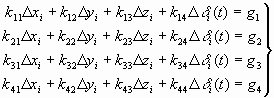 (21)
(21)