

Article of the Month - March 2021 |
 |
 |
 |
|
 |
| Greet Deruyte | Lars De Sloover | Jeffrey Verbeurgt | Alain De Wulf | Sander Vos |
This article in .pdf-format (13pages)
This article was included in the proceedings of FIG Working Week 2020. Knowledge on natural sand dynamics is essential and the authors present first results achieved with currently used methodology. Next, they analyze the results from a 10-day measurement campaign and highlight the tide-dominated beach morphology.
In order to protect the Belgian coast, knowledge on natural sand dynamics is essential. Monitoring sand dynamics is commonly done through sediment budget analysis, which relies on determining the volumes of sediment added or removed from the coastal system. These volumetrics require precise and accurate 3D data of the terrain on different time stamps. Earlier research states the potential of permanent long-range terrestrial laser scanning for continuous monitoring of coastal dynamics. For this paper, this methodology was implemented at an ultradissipative macrotidal North Sea beach in Mariakerke (Ostend, Belgium). A Riegl VZ-2000 LiDAR, mounted on a 42 m high building, scanned the intertidal and dry beach in a test zone of ca. 200 m wide on an hourly basis over a time period of one year. It appeared that the laser scanner could not be assumed to have a fixed zenith for each hourly scan. The scanner compensator measured a variable deviation of the Z-axis of more than 3.00 mrad. This resulted in a deviation of ca. 900 mm near the low water line. A robust calibration procedure was developed to correct the deviations of the Z-axis. In this paper, we start by presenting the first results achieved with the current methodology. Next, we analyze the results from a 10-day measurement campaign and highlight the tide-dominated beach morphology.
Terrestrial LiDAR (Light Detection And Ranging) technology makes it possible to collect high resolution, accurate and instantaneous topographic data of large areas. In the last decade, terrestrial laser scanning (TLS) has been more and more used to study aeolian and coastal geomorphology (Almeida et al., 2013; Huising & Gomes Pereira, 1998; Montreuil, Bullard, & Chandler, 2013; Pye & Blott, 2016).
Lindenbergh et al. (Lindenbergh, Soudarissanane, de Vries, Gorte, & de Schipper, 2011) presented short-range static terrestrial laser scanning on a beach to identify morphodynamic changes at the sub-centimeter level. More recently, Anders et al. and Vos et al. (Anders et al., 2019; Vos, Lindenbergh, & De Vries, 2017) described the use of permanent TLS (range < 300 m) for continuous (hypertemporal) monitoring of coastal change. Their study set-up determined a precision in terms of a standard deviation of 1.5 cm between two-consecutive scans.
The study area and system configuration of the laser scanner are elaborated in the second section. The third section describes the different alignment and calibration methods used. Section 4 assesses the results of the calibration procedures as well as some findings from a 10-day case study.
In this study, the methodology developed by Vos et al. (Vos et al., 2017) was implemented at the North Sea beach of Mariakerke (Ostend, Belgium) (figure 1 & figure 2 – left panel) using a Riegl® VZ-2000 terrestrial laser scanner. A seawall (figure 1) and a groin field (200 m between each groin) with regularly carried out beach and underwater nourishments characterize this beach. It is gently sloping (1 – 2 %) and ultra-dissipative (Deronde, Houthuys, Henriet, & Van Lancker, 2008), consisting of medium and coarse sand with an average grain size of 310 µm. The Belgian coast is situated in a macro-tidal regime ranging from 3.5 m at neap tide to 5 m at spring tide. The area of interest is bordered by the two groins and the seawall. Over the past few years, this beach has been the subject of frequent mobile and static terrestrial LiDAR surveys (De Wulf, De Maeyer, Incoul, Nuttens, & Stal, 2014; Stal et al., 2014).

Figure 1. Mariakerke Beach and its typical seawall at mid-tide.
In our field set-up, the vertical axis of the laser scanner appears to have a certain variability between hourly scans of more than 3.00 mrad, resulting in a shift of more than 0.9 meter at the low water line. The aim of this study was to develop a robust and automated alignment procedure to adjust both the hourly and fixed deviations of the scanner’s zenith. The final objective is to examine which combination of calibration parameters yields the best results.

Figure 2. Map of the study area (left), Riegl® VZ-2000 TLS overlooking the beach (right)
A time-of-flight pulse-based laser scanner, mounted on a 42 m high building near the study area (figure 2, right panel), scanned the intertidal and dry beach. The scanner was installed on a stable frame and protected by weather-proof housing. The exact scanner location was determined through Real-Time Kinematic Global Navigation Satellite System (RTK-GNSS) positioning. Data acquisition took place on an hourly base from 8 November 2017 to 6 December 2018.
The deviation of the vertical axis of the scanner required the development of a robust and automated calibration procedure to correct both the hourly and fixed deviations of the scanner’s Z-axis. The variables of the problem are the inclination of the Z-axis in two different preferably independent directions. For easy intuitive interpretation, the orthogonal directions of the seawall (X-axis) and the groin (Y-axis) were selected.
A static scan produces a dense point cloud, containing around four million points, with approximately one million situated on the seawall and groin, one million points on the dry beach and one million in the intertidal zone. Environmental constraints (e.g. high humidity of the surface, rain, fog, snow or high tide) yield smaller point sets on the beach.
The actual calibration procedure is done by making a 2.5D model of each static scan and registering it to a ‘truth’ set of reference points. The robustness of the alignment implies that the calibration procedure must approximate the following ideal situation:
For the scan-based model, two main approaches were used:
For the choice of truth, three sets of reference points were available:
Figure 4 shows the workflow applied. Either a TIN model or a gridded model of the static scan was made. In case of the TIN-approach, the difference between the scan model and the truth set is the height difference between individual points of the reference set and the corresponding triangle of the TIN-model of the scan. In the grid-approach, grids of both the scan and the reference set were made. However, the static scan yields different point densities at the end of the groin compared to the end of the seawall. For this reason, the interval distance for the rasterizing was chosen differently in the seawall zone compared to the groin zone to obtain a balanced calibration set in the x- and y-direction. Next, using a Monte Carlo simulation with multiple rotational values, the difference between the scan model and the reference set was minimized. From an angle of -5 mrad till + 5 mrad, 1001 x-axis rotational values are combined with 1001 y-axis rotational values in steps of 0.01 mrad.
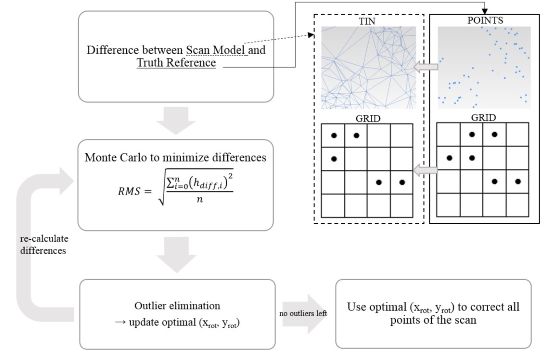
Figure 4. Workflow of the calibration algorithm.
Each static scan is expected to contain outliers. The outliers originate mainly from ghosting (e.g. people and obstacles on the seawall and groin that are scanned). These outliers yield elevation values that are significantly higher than the true surface. A severe outlier test is needed, but eliminating too many values gives a too optimistic value in terms of calibration quality. A point i of the reference set is an outlier if

Finally, a sigma rule of thumb is applied, considering a width of 2, 2.5 and 3 standard deviations around the mean. After each elimination of outliers, an optimal x- and y-rotation are computed, yielding slightly different values as the reference set was modified in the previous step and subsequently a new outlier test is performed. This iterative process continues till no more outliers are detected. If no more outliers can be detected, all the points of the static scan are corrected with the optimal x- and y-rotation.
Table 1 gives an overview of the calibration quality statistics per model of the static scan and model parameter applied for a first series of calibration runs with a selection of the 50 most accurate points in the truth. The mean of algebraic differences (MEAN), the mean of absolute differences and the RMS are calculated for each model parameter individually. Per static scan model and per parameter, the applied rotation around the x- and y-axis are given.
Table 1. Static scan models and parameters applied –mean of algebraic differences (MEAN), mean of absolute distances, RMS, and x- & y-axis rotation for a first series of calibration runs.
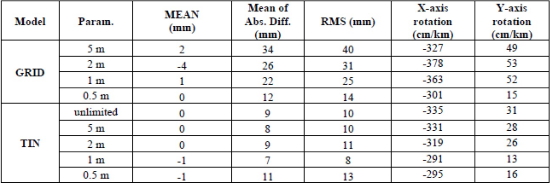
The TIN models (5 m, 2 m, 1 m and unlimited edge size) perform best in all categories. From here on, these models were used in the quest for the best reference set and the optimal outlier elimination strategy. For each reference set, the three-sigma (2, 2.5 and 3 standard deviations) outlier elimination tests were done plus a test without outlier elimination. In order to make a clear and easy comparison, one weighted (considering all TIN parameters) RMS (figure 5, panel A) were calculated for all outlier elimination strategies per reference set.
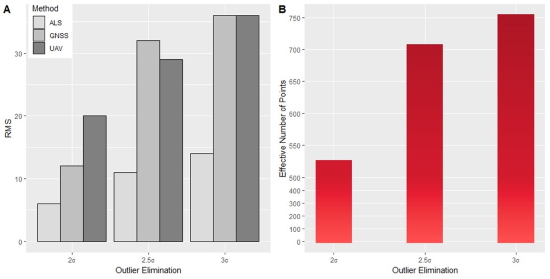
Figure 5. Visualization of RMS as a function of n·sigma per reference set (A) and number of effective points used as a function of n·sigma for the ALS reference set (B).
Figure 5 (B) shows the effective number of points used per outlier elimination strategy for the ALS reference set. An outlier elimination strategy of 2.5σ gives a good overall result with not too many points eliminated and sufficient effective points remaining.
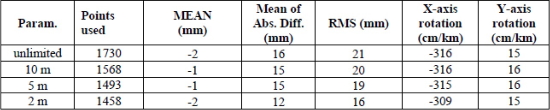
Table 2 gives an overview of the MEAN, Mean of Absolute Differences, RMS and x- & y-axis rotation for different edge limit values of the TIN model, calibrated on the ALS truth with 2.5σ outlier removal.
Table 2. Statistics of the calibration procedure for different TIN sizes
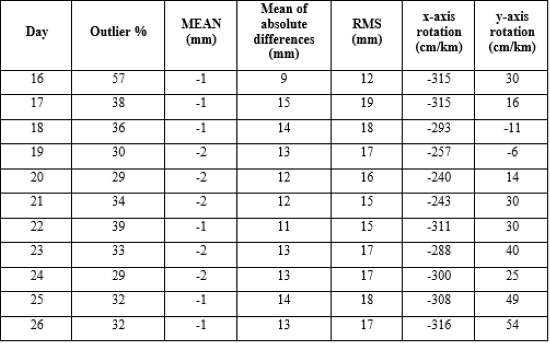
As a case study, calibration results of a 10-day measurement campaign from 16 April 2018 till 26 April 2018 were analyzed. Different parameters were taken into consideration, including outlier percentage (effective number of points used divided by the initial amount of points in the point cloud), mean of algebraic differences, mean of absolute differences, RMS and x- and y-axis rotation. The results of this 10-day study are presented in Table 3.
Table 2. Statistics of the calibration procedure for 10 consecutive days.
During this campaign, meteorological conditions (both aeolian and hydrodynamic forcing) were observed at the nearby Ostend Meteo Park and the Raversijde Waverider Buoy. Wind and wave data of the 10-day period are presented in figure 6 and 7 below.
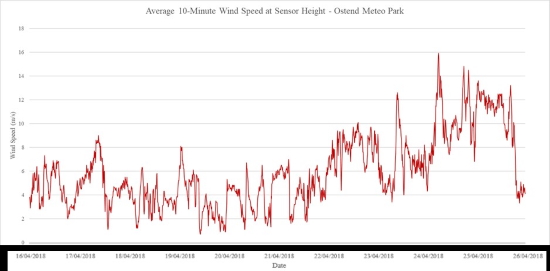
Figure 6. Results from wind speed measurements (temporal resolution = 10 minutes) at the Ostend Meteo Park.
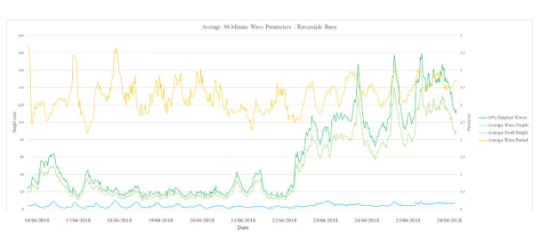
Figure 7. Results from wave measurements (temporal resolution = 30 minutes) at the Raversijde Buoy.
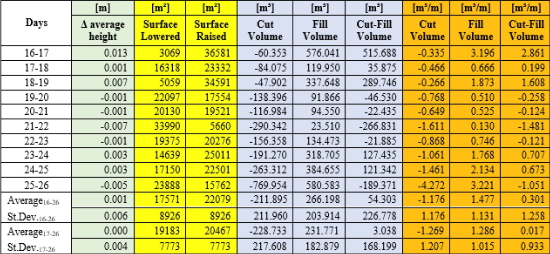
Additionally, volume changes within a fixed study area were determined between the first (16 April 2018) and last day (26 April 2018) of the campaign, using a so called planimetric method, based on the TIN-interpolated scan model. Table 3 below shows the change in daily average height of the beach surface within the study area, as well as the daily changes in volume.
Table 3. Changes in volume and average height of the beach surface in-between consecutive days.
The higher the resolution of the grid model, the more accurate the computation of the difference in heights between the static scan model and the reference points. The smaller the cell / edge limit value, the more holes in the model, the less reference points can be interpolated in the model, reducing the quantity and therefore the validity of the difference point set. Overall, the TIN model yields the most means of algebraic differences close to zero, this is thus a good measure of accuracy. The TIN-model (10 m, 5 m, 2 m and unlimited edge size) has the smallest mean of algebraic differences and the smallest RMS and are therefore the most precise (repeatable) models with the smallest random error.
Hence, for further processing, only the TIN-model with 10 m, 5 m, 2 m and unlimited edge size were considered. On one hand, it can be easily concluded that the ALS truth yields the best overall RMS for all TIN models together (figure 5-A). It shows on the other hand that the GNSS reference set with 2σ elimination returns a similar RMS. Figure 5-B however shows that the outlier removal percentage for 2σ is way higher than 2.5σ with both GNSS and ALS. Moreover, less points available in the reference set, reduces the quantity and therefore validity of the calibration.
When looking closer at the results (table 2) for different edge limit values of the TIN with 2.5σ outlier elimination and ALS truth, several remarks can be made. The applied rotation (in both directions) is more or less the same for all edge limit values. The TINs with smaller edge limit values produce a lower RMS and mean of absolute differences but yield a smaller reference set available for the model interpolation. At the same time, the TINs with bigger edge limit values have less points eliminated, but come with a higher RMS and mean of absolute differences. A TIN with 5 m edge limit value seems to be the middle ground with an RMS of 19 mm, and an accuracy of 15 mm.
Interpretation of the aeolian and hydrodynamic forcing shows calm conditions during the first days (16 till 21 April) with wave heights below 80 centimeters and wind speeds only incidentally exceeding the 7 m/s threshold for aeolian transport. Swell and wave period conditions remain constant throughout the entire 10-day period. From 22 April till 26 April, wind speeds exceeded the 7 m/s on a few occasions and average wave heights were as high as 140 centimeters (with outliers reaching up to 180 centimeters).
An analysis of Table 2 (reporting the day-to-day calibration results) leads to a number of conclusions. First of all, the x-axis deflection varies between -316 and -240 cm/km with a maximal daily variation of 68 cm/km. Y-axis deflections vary between -11 and 54 cm/km with a maximal daily variation of 27 cm/km. A trendline nor a correlation with aeolian forcing could, at first sight, not be detected.
When looking at the RMS values of the differences between the reference aerial LiDAR point cloud and the calibrated static scan TIN model, variations between 12 and 19 mm occur. The lowest RMS (12 mm) was observed on the first day. This can be explained by a lower number of reference points that could be interpolated in the TIN model. 16 April was a rainy day, leading to a sparser coverage scan points on the dike and groin.
Finally, it appears that the daily means of absolute deviations are not symmetrically distributed around zero. The static scan model lies systematically above the height of the reference data sets, which is to be expected as obstacles (e.g. ghosting) are all above the surface of the dike and groin reference points.
The volume changes in our area of interest during the campaign are small. Between the first (16 April) and last day (26 April), there is an increase in average height of the beach of 14 mm. The maximum difference between successive days is 13 mm between 16 April and 17 April, corresponding to a net volume change of + 515.688 m³ or 2.861 m³/m. Between the other successive days, the maximum absolute difference of the average height is only 7 mm with a standard deviation of differences of 4 mm. When ignoring the first day; the net volume change between successive days varies between -1.481 m³/m and + 1.608 m³/m, yielding an average cut-fill volume of just (0.017 ± 0.933) m³/m.
Despite the calm environmental forcings during the first days of the campaign, a significant change of the beach topography occurs. The last days of the campaign are characterized by higher waves and stronger winds. However, no significant changes in beach topography take place.
When looking at the tides; spring tide occurred at 16 April. It appears the highest changes in intertidal beach topography take place during more extreme tidal conditions. When the tidal conditions are ‘calm’, beach topography remains the same, despite higher waves and stronger winds.
Recently, terrestrial LiDAR and permanent TLS have been more and more used to monitor coastal morphodynamics. However, these sorts of experiments come with the demand for an accurate calibration. In this study, a robust and automated alignment procedure was developed to correct deviations of the scanner’s zenith. Besides, each static scan is expected to contain altimetric outliers, originating from ghosting. Different 2.5D models of one scan were registered to different sets of reference points. Ultimately, several iterative outlier elimination procedures were tested. Modelling the static scan into a TIN with triangle edge sizes no longer than 5 metres yielded the best results for a calibration on the ALS reference data set. A 2.5σ outlier elimination gave the best accuracies. As a case study, a 10-day measurement campaign was set up. During this campaign, both spring and neap tide took place. Calm wave conditions without wind occured as well as stronger winds and higher waves. Finally, it can be assumed that during the period of 17 – 26 April no significant volume changes took place on the beach and that any (small) variation in beach topography is due to measurement errors of the LiDAR. Future research will focus on the processing of multi-temporal scan series with a view to the detection of coastal morphological features.
MSc Lars De Sloover
Ghent University, Department of Geography
Krijgslaan 281 (S8 Building)
9000-GhentBELGIUM
Web site:
www.geografie.ugent.be/members/802002047140
Prof. dr. ing. Greet Deruyter
Ghent University, Department of Civil Engineering
Msc Lars De Sloover
Ghent University, Department of Geography
Msc Jeffrey Verbeurgt
Ghent University, Department of Geography
Prof. dr. ir. Alain De Wulf
Ghent University, Department of Geography
Dr. ir. Sander Vos
Delft Technical University, Department of Hydraulic Engineering, the
Netherlands
Email: [email protected]